By Don Carona
If you've been involved in astronomy for even a short time, it's likely you are familiar with the Equatorial Coordinate System: Right Ascension (RA) and Declination (DEC). Right ascension is the equivalent of celestial longitude and declination the equivalent of celestial latitude.
Did you know there is another member of the equatorial coordinate system: Hour Angle (HA)? The hour angle is an alternative to right ascension. It is measured westward from the meridian which is a little backwards compared to right ascension. Hour angle is primarily used to measure the time since an object last transited (crossed) the meridian plane (middle of the sky). This is also known as reaching upper culmination.
As an aside, it wasn't that long ago that the controllers for most telescope mounts were hour angle based instead of right ascension based for the longitudinal axis movement. The venerable Boller & Chivens mounts of the late 40's to the early 70's used an hour angle dial on the main control board instead of right ascension.
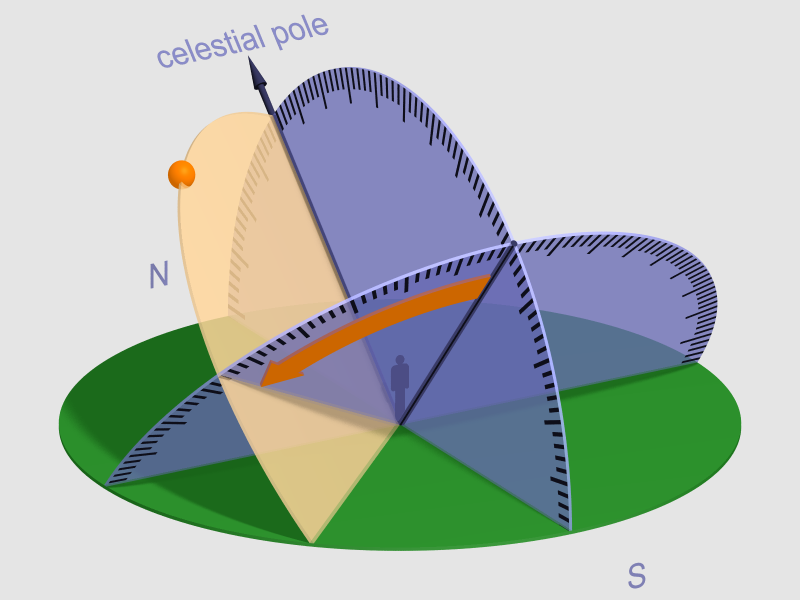
The hour angle (orange arrow on the celestial equator plane) ends at the hour circle of an orange dot (apparent place of an astronomical object on the celestial sphere). Image Attribution - Sch, CC BY-SA 3.0, via Wikimedia Commons
The hour angle is still in the machine so-to-speak, we just don't see it come up very often. Instead, we see right ascension in our desktop planetarium programs or mount control software. This is most likely because to calculate the hour angle, you have to know the right ascension of the object and the local sidereal time. This can make determining the hour angle a little complicated and the result can be ambiguous if used incorrectly. Regardless, it is an excellent means of determining when an object will rise, transit and set to within a few minutes without having to do any programming.
Let's get into it. Hour angle is referenced from Greenwich, England. The local hour angle (LHA) is the measurement from the observer's geographic position, which is what we are generally interested in knowing. The local hour angle can be expressed mathematically as the local sidereal time minus the right ascension of an object.
The local hour angle can be expressed in either degrees or time depending on need. Recall that each hour of right ascension is equal to 15 degrees. Therefore, if you want to express the local hour angle in degrees, you must ensure that both the local sidereal time and the right ascension are converted appropriately. When measured in degrees, the local hour angle yields the position of the object on the celestial sphere measured westward from the meridian.
We could spend a day learning about local sidereal time (LST). A simplification of it can be stated as the right ascension currently at the local meridian i.e.(time by the stars). Let's say you go outside and face due south. You realize that bright star Sirius is in the middle of the sky (on the meridian). The right ascension of Sirius is 06h 45m 08.917s. Therefore, LST = 06:45:08.917.
Let's calculate the local hour angle of an object for a given moment in time. To be very clear about what we want to measure, I've added some steps:
1. LHA = LST - RA
2. IF (LHA < 0) {LHA = LHA + 24}
3a. Next Transit = 24 - LHA
- OR -
3b. IF (LHA > 12) {LHA = LHA - 24}
It should be noted that according to many references, a (-) negative value resulting from Step 1 represents the time until the next transit. However, this is ambiguous. For instance, if LST ≈ 0h, all values for LHA will be negative regardless of where they are on the celestial sphere. If LST ≈ 23h, almost all eastward (object is rising) values will be (+) positive and would represent the time since the last transit. Step 2 corrects this to the time since the last transit and Step 3a inverts it to the time until the next transit.
Here is a breakdown of each step:
Step 1:This is the initial calculation for the local hour angle.
Step 2: This is the corrective step to unambiguously determine how much time has elapsed since the object's last transit.
Step 3a: (optional): This step will yield how much time must elapse before the object will transit again.
Step 3b: (optional): In order to keep with tradition and display a value as (-) negative for rising objects and (+) positive for setting objects, use this equation instead of Step 3a. An object with a LHA = -6 is on the eastern horizon; LHA = 0 is on the meridian; and LHA = +6 is setting on the western horizon.
Example: Determining the local hour angle can give us an idea of when an object will rise, transit and set. M42 (Great Nebula in Orion) is located at RA 05h 35m 16.8s. What time will M42 rise above the horizon if you are observing from the Brazos Valley on August 21st at 8:00 P.M. local time?
1. LST on August 21st @ 8 P.M. = 16h 34m 53s = 16.5814394827
2. Determine the LHA.
M42 RA = 05h 35m 16.8s = 5.0 + (35.0 / 60.0) + (16.8 / 3600.0) = 5.588
LHA = 16.5814394827 - 5.588 = 10.9934394827 ≈ 11h
(This is how much time has elapsed since M42's last transit.)
3. Determine how much time will elapse before the next transit.
Hours To Next Transit = 24h - 11h = 13h
4. Determine the time of the next transit.
Transit = 8 P.M. + 13h ≈ 9:00 A.M. on August 22nd
5. Subtract 6 hours from the Step 4 result to determine when M42 will be on the eastern horizon.
Rise = 9:00 A.M. - 6h ≈ 3:00 A.M. on August 22nd
6. Add 6 hours to the Step 4 result to determine when M42 will set.
Set = 9:00 A.M. + 6h ≈ 3:00 P.M. on August 22nd
There you have it. The rise, transit and set times for M42 on August 22nd. The results are low accuracy, but should be within ~15 minutes of the true event times. Consider this method a rough estimate. The reason the results aren't a higher accuracy is that this method ignores the object's true declination and assumes it's on the celestial equator. To include the declination of the object would mean having to use a computer or calculator to get the answer, but that wasn't really our goal. We just needed a "good idea" of when to expect these events.
For the sake of completeness and for those with a little programming savvy, I have written a small C++ program that takes the declination into account. This will give you a good idea of how to implement it and arrive at more accurate results. It still isn't high accuracy, but should be good to within a couple of minutes.
Link to C++ Program
https://doncarona.tamu.edu/assets/hourangle/hourangleevents.cpp
If you use the C++ program for other objects, be sure to change the equatorial coordinates; time zone offset; and the JD. If you want to use the current JD, uncomment Line 54 and comment out Line 55. You can make the program better as well by getting the current time zone offset programmatically. I'll leave that up to you. I implemented two methods to get the local event times, read the comments to understand their functionality.
Results from the C++ program using the same date from our example above.
The table in the link below notes the local sidereal time (LST) at 8:00 P.M. for the Central Time Zone for each day in 2023. The table accounts for Central Daylight Time (CDT). Add 1 hour for each hour after 8 P.M. Subtract 1 hour for each hour before 8 P.M.
** Print a copy and store with your astronomy equipment for easy reference in the field.
CST Local Sidereal Time Lookup Table
About the Author:
Don has been involved with the Physics Teaching Observatory at Texas A&M University for more than 3 decades, designing both the facilities and the programs. He also works with college observatory programs at several universities in the U.S. Observational data collection is a passion and he has been instrumental in the photometry of the bright star, Betelgeuse. When not looking at the sky, Don is an avid programmer.
Website: https://DonCarona.tamu.edu/
Contact: don@tamu.edu
Spring 2023 Newsletter
CONTACT EMAIL:
contact@brazosvalleyastronomyclub.org
Coordinator - Randy Light, M.D.
PROGRAM REQUEST EMAIL:
outreach@brazosvalleyastronomyclub.org
Coordinator - Tom Campbell
GOOGLE DISCUSSION GROUP:
https://groups.google.com
Coordinator - Randy Light, M.D.
WEBSITE AND NEWSLETTER EMAIL:
webmaster@brazosvalleyastronomyclub.org
Coordinator - Ginger Wentrcek
Follow Us on Facebook
Member: Astronomical League
Member: Night Sky Network
BVAC Website:
https://brazosvalleyastronomyclub.org
© Brazos Valley Astronomy Club
The Brazos Valley Astronomy Club is a non-profit group
located in Bryan-College Station, Texas.
Our goal is to promote astronomy and related science
as a hobby for people of all ages.